I’ve recently been investigating the command-line utility zfec, which is a lot like the UNIX “split” utility, except, using a technique called erasure coding, you can choose to split your file into M pieces, any K of which are enough to recreate the file using the complimentary [sic] zunfec command.
Concrete example: a 100K file can be split into 10 (or more) pieces, each just over 25K long, and zunfec can recreate the original from any 4 of them.
Any 4. You might expect this to incur a lot of overhead in each piece, but it turns out it’s just a header of four bytes or less. Pretty much the same as cutting the file into pieces.
This amazed me. How could this possible work? How can you split data into M pieces so that any K of them is enough to reconstruct them? Linear algebra to the rescue!
Suppose we want to encode a twelve character text string into a bunch of arrays, each with four values, any three of which are sufficient to reconstruct the original. Let’s use the string “Lovefromdawn”. Here’s what you do:
The matrix furthest to the left is a Vandermonde matrix, which is a matrix where each row forms a geometric series starting with 1. A square Vandermonde matrix has the special property that as long as the second column has no repeated elements, the matrix is invertible (and in fact, there is a special algorithm to invert it quickly).
The split pieces correspond to rows of the matrix on the right. Choose any three of them; let’s say row 1, 2 and 4. Once we know what row numbers they are (and this explains the tiny header), we get the following system of equations:
We know the leftmost matrix is invertible, so multiply both sides by the inverse, and we solve for X, recovering “Lovefromdawn”. Wowza!
But wait! One problem remains: if we use standard integer arithmetic, the matrix on the right ends up with a lot of values larger than 255, and we can’t store it in a byte array. That ain’t no good.
Luckily, it turns out that most theorems dealing with matrices and invertibility only assume we are operating over an arbitrary field, a mathematical structure that has addition, a 0, multiplication, a 1, and a reciprocal for every non-0 element.
Abstract algebra to the rescue! (Math seems to rescue computer science a lot.) It turns out that there is a field with 256 elements known as GF(2**8). In this field, 0 is the 0, 1 is the 1 (surprise!), addition is bitwise exclusive-or (so every number is its own additive inverse!), and multiplication is a weird, and seemingly unpredictable beast, that is best calculated by pre-populating a table of logarithms and exponents, then creating a 256×256 array containing the multiplication table (since each number fits in a byte, the whole table only takes 64K).
[There are actually lots of ways to define multiplication that still meets the requirements of a field, but we have to pick one by defining what’s called the irreducible polynomial for the field.]
Once we operate over this field, all matrix values are guaranteed to be in the range [0, 255], and our method for bytewise encoding and decoding becomes easy.
One more aside: zfec actually piles the 3×3 (well, KxK) identity matrix on top of the Vandermonde matrix, so the first K pieces are exactly what you’d get by cutting the file into K pieces in the obvious way and putting the tiny header in front. Even though our matrix is no longer a Vandermonde matrix, submatrices are still guaranteed to be invertible and it still works.
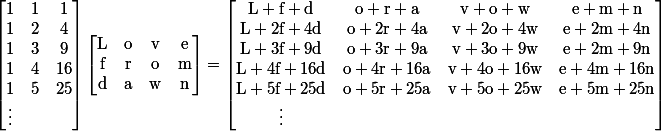
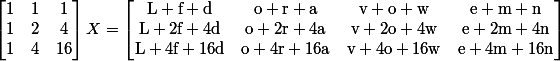
I ? math.
> I’ve recently been investigating the command-line utility zfec, which is a lot like the UNIX “split” utility, except, using a technique called erasure coding, you can choose to split your file into M pieces, any K of which are enough to recreate the file using the complimentary zunfec command.
par2 is insanely useful for backups onto optical disks. One file was corrupted? No problem! We’ll just recover using the par2 FEC we made back when we did the original backup…
(I use par2 rather than zfec because, even though it’s way slower, it’s already been around for like a decade and I’m not sure how maintained or robust zfec is.)
Any specific reason for using ordinary Reed-Solomon over Cauchy Reed-Solomon? The latter is generally considered to be much faster for several reason, one being that multiplication is reduced to a series of XOR-operations.
This is cool. Each offset (a byte in the chunk) is composed of multiple bytes from the original string with a stride of said offset, and you use matrix inversions to reconstruct the original.
Great! What a nice math breeze in the CS world.
Hi, I’ve invented an algorithm which fulfils a similar purpose to zfec (I did not know about zfec, erasure codes or fountain codes at the time).
http://www.reddit.com/r/programming/comments/1kq70k/holographic_views_of_data/
If you would like to talk about this, please feel free to email me.
can u suggest me the code in java for splitting the file into chunks when uploaded to the server