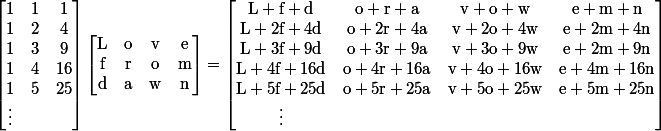BIP0032 defines a way to create a hierarchical deterministic wallet (that is, a way to create an entire tree of Bitcoin addresses and private keys) through a tree of wallet key nodes.
Each node has a public and private key associated with it, which can be displayed as a Bitcoin address and a WIF string. But each node also has additional entropy information, called the “chain code”, which gets fed back into the algorithm that generates the children, so revealing even the WIF doesn’t give enough information to reveal the children.
A node can be stripped of private key information, yielding a public key node. These nodes can only generate the Bitcoin address, and not the WIF. But they can still generate half of the child nodes. But only the public key node versions. So once you strip out the private-ness from a node, it’s gone forever.
Each node element can be represented by a 111-digit base58 number that looks like this:
xprv9s21ZrQH143K3QTDL4LXw2F7HEK3wJUD2nW2nRk4stbPy6cq3jPPqjiChkVvvNKmPGJxWUtg6LnF5kejMRNNU3TGtRBeJgk33yuGBxrMPHi
xpub661MyMwAqRbcFtXgS5sYJABqqG9YLmC4Q1Rdap9gSE8NqtwybGhePY2gZ29ESFjqJoCu1Rupje8YtGqsefD265TMg7usUDFdp6W1EGMcet8
Keys for the main network start with “xprv” (private) or “xpub” (public).
A node has 2^32 children, enumerated 0, 1, 2 .. 4294967295. Children with index at least 2^31=2147483648=0x80000000 are derived using “prime” or “private key” derivation, and can only be generated by the private wallet key. We use the shortcut 2p or 2’ to indicate child number 2+0x80000000.
A “key path” is a route down the tree. It’s a “/”-separated list of numbers, where each number can optionally have a trailing p or ’ character to indicate “prime”. (Typing “p” is much easier than “’” which needs to be escaped or quoted in the shell.)
Example key paths: “1”, “0/2p”, “0p/1000/5”, “0/0/0/0/0/37”.
Reading the BIP0032 is a hard slog. Maybe some examples will make this clearer. I’ve created a script for now called genwallet (I know, I know, I need a better name) that lives in my pycoin project. Create a virtualenv and install it. This has been tested with Python 3.3 but should work in Python 2.7 too. There may be minor discrepencies in what you see here and what you see on your terminal if you follow along, as this project has been undergoing heavy changes lately. Forgive me.
$ virtualenv pycoin.env
$ source pycoin.env/bin/activate
$ pip install pycoin
Downloading/unpacking pycoin
Downloading pycoin-0.15.tar.gz
Running setup.py egg_info for package pycoin
Installing collected packages: pycoin
Running setup.py install for pycoin
Installing genwallet script to (...)/pycoin.env/bin
Successfully installed pycoin
Cleaning up...
You create the top node of a tree by feeding it entropy.
$ head -c200 /dev/random | genwallet -
xprv9s21ZrQH143K3wqna1KnwoSH3reKVVp68cAuJ4izQMMe7VvzBcFdnxYvtMifigMDynsTzCSiLvCt2ksKYrSY4m5z2AQc7g7vZL6uvdaSiBn
Your results may vary. Hopefully.
Let’s use a known key so we can check our results. BIP0032 has some test vectors. Let’s try the first one.
$ python -c 'import binascii; open("master-private-key-entropy", "w+b").write(binascii.unhexlify("000102030405060708090a0b0c0d0e0f"))'
$ hd master-private-key-entropy
00000000 00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f |................|
00000010
This is the initial entropy for test vector #1. Don’t use any of these key address for real storage of Bitcoin, since the private keys are all over the internet. All right? Good.
$ genwallet master-private-key-entropy > master-private-key
$ cat master-private-key
xprv9s21ZrQH143K3QTDL4LXw2F7HEK3wJUD2nW2nRk4stbPy6cq3jPPqjiChkVvvNKmPGJxWUtg6LnF5kejMRNNU3TGtRBeJgk33yuGBxrMPHi
It matches the test vector! How about the public key? Use -s to pass in the key path. We use a trick here that the “.pub” suffix means “strip down to public key only by stripping out secret exponent information”. And that an empty key path stays on the current node. (Ugh. Need to add a -P flag.)
$ genwallet -f master-private-key -s .pub > master-public-key
$ cat master-public-key
xpub661MyMwAqRbcFtXgS5sYJABqqG9YLmC4Q1Rdap9gSE8NqtwybGhePY2gZ29ESFjqJoCu1Rupje8YtGqsefD265TMg7usUDFdp6W1EGMcet8
That matches the test vector too! Let’s generate the rest of them.
$ genwallet -f master-private-key -s 0p.pub
xpub68Gmy5EdvgibQVfPdqkBBCHxA5htiqg55crXYuXoQRKfDBFA1WEjWgP6LHhwBZeNK1VTsfTFUHCdrfp1bgwQ9xv5ski8PX9rL2dZXvgGDnw
$ genwallet -f master-private-key -s 0p
xprv9uHRZZhk6KAJC1avXpDAp4MDc3sQKNxDiPvvkX8Br5ngLNv1TxvUxt4cV1rGL5hj6KCesnDYUhd7oWgT11eZG7XnxHrnYeSvkzY7d2bhkJ7
$ genwallet -f master-private-key -s 0p/1.pub
xpub6ASuArnXKPbfEwhqN6e3mwBcDTgzisQN1wXN9BJcM47sSikHjJf3UFHKkNAWbWMiGj7Wf5uMash7SyYq527Hqck2AxYysAA7xmALppuCkwQ
$ genwallet -f master-private-key -s 0p/1
xprv9wTYmMFdV23N2TdNG573QoEsfRrWKQgWeibmLntzniatZvR9BmLnvSxqu53Kw1UmYPxLgboyZQaXwTCg8MSY3H2EU4pWcQDnRnrVA1xe8fs
$ genwallet -f master-private-key -s 0p/1/2p.pub
xpub6D4BDPcP2GT577Vvch3R8wDkScZWzQzMMUm3PWbmWvVJrZwQY4VUNgqFJPMM3No2dFDFGTsxxpG5uJh7n7epu4trkrX7x7DogT5Uv6fcLW5
$ genwallet -f master-private-key -s 0p/1/2p
xprv9z4pot5VBttmtdRTWfWQmoH1taj2axGVzFqSb8C9xaxKymcFzXBDptWmT7FwuEzG3ryjH4ktypQSAewRiNMjANTtpgP4mLTj34bhnZX7UiM
$ genwallet -f master-private-key -s 0p/1/2p/2.pub
xpub6FHa3pjLCk84BayeJxFW2SP4XRrFd1JYnxeLeU8EqN3vDfZmbqBqaGJAyiLjTAwm6ZLRQUMv1ZACTj37sR62cfN7fe5JnJ7dh8zL4fiyLHV
$ genwallet -f master-private-key -s 0p/1/2p/2
xprvA2JDeKCSNNZky6uBCviVfJSKyQ1mDYahRjijr5idH2WwLsEd4Hsb2Tyh8RfQMuPh7f7RtyzTtdrbdqqsunu5Mm3wDvUAKRHSC34sJ7in334
$ genwallet -f master-private-key -s 0p/1/2p/2/1000000000.pub
xpub6H1LXWLaKsWFhvm6RVpEL9P4KfRZSW7abD2ttkWP3SSQvnyA8FSVqNTEcYFgJS2UaFcxupHiYkro49S8yGasTvXEYBVPamhGW6cFJodrTHy
$ genwallet -f master-private-key -s 0p/1/2p/2/1000000000
xprvA41z7zogVVwxVSgdKUHDy1SKmdb533PjDz7J6N6mV6uS3ze1ai8FHa8kmHScGpWmj4WggLyQjgPie1rFSruoUihUZREPSL39UNdE3BBDu76
The -i flag dumps out a bunch of extra info.
$ genwallet -f master-private-key -s 0p/1/2p/2 -i
xprvA2JDeKCSNNZky6uBCviVfJSKyQ1mDYahRjijr5idH2WwLsEd4Hsb2Tyh8RfQMuPh7f7RtyzTtdrbdqqsunu5Mm3wDvUAKRHSC34sJ7in334
main network
private key
secret exponent: 6911148411995144978760870745829922996940679624545579157337939690887778291444
public pair x: 105057282133830096634347636156404839657295714659718969275583812905733562047785
public pair y: 17712072790142815456499743834226465136387452166901773802686902612896636999328
tree depth: 4
fingerprint: d880d7d8
parent f'print: ee7ab90c
child index: 2
chain code: cfb71883f01676f587d023cc53a35bc7f88f724b1f8c2892ac1275ac822a3edd
WIF: KwjQsVuMjbCP2Zmr3VaFaStav7NvevwjvvkqrWd5Qmh1XVnCteBR
uncompressed: 5Hw1ss3oPLXfyYSZrxQr4xFrpq7nEaX5HkSnxdAXuWcM4JEio8S
Bitcoin address: 1LjmJcdPnDHhNTUgrWyhLGnRDKxQjoxAgt
uncompressed: 1FzKW1LPEjEeRamxYR8oxVPLFJt525Nffm
$ genwallet -f master-private-key -s 0p/1/2p/2/1000000000 -i
xprvA41z7zogVVwxVSgdKUHDy1SKmdb533PjDz7J6N6mV6uS3ze1ai8FHa8kmHScGpWmj4WggLyQjgPie1rFSruoUihUZREPSL39UNdE3BBDu76
main network
private key
secret exponent: 32162737660659799401901343156672072893797470137297259782459076395168682141640
public pair x: 19122724810578381401279259492091176497647579703487086604820598127878910996497
public pair y: 93716738155005567718020901196556981584525395439024483644561058920479008416610
tree depth: 5
fingerprint: d69aa102
parent f'print: d880d7d8
child index: 1000000000
chain code: c783e67b921d2beb8f6b389cc646d7263b4145701dadd2161548a8b078e65e9e
WIF: Kybw8izYevo5xMh1TK7aUr7jHFCxXS1zv8p3oqFz3o2zFbhRXHYs
uncompressed: 5JMbvQZXHJAzJyoDnqWasGCwtiHJZivF2ckjn3n5mazYYtGNvJf
Bitcoin address: 1LZiqrop2HGR4qrH1ULZPyBpU6AUP49Uam
uncompressed: 1N7NsvfJJqhjjFp5R2X9FmBc8MLU7gxbsL
Note how the second example suggests that the first example is its parent by identifying its fingerprint, and having a depth that’s one deeper.
We can feed the key on the command-line too using -k (although it’s a bad idea for real keys, since it exposes it in ps and your shell’s history). Every bit of this data is encoded in the 111-character wallet key.
$ genwallet -i -k xprvA41z7zogVVwxVSgdKUHDy1SKmdb533PjDz7J6N6mV6uS3ze1ai8FHa8kmHScGpWmj4WggLyQjgPie1rFSruoUihUZREPSL39UNdE3BBDu76
xprvA41z7zogVVwxVSgdKUHDy1SKmdb533PjDz7J6N6mV6uS3ze1ai8FHa8kmHScGpWmj4WggLyQjgPie1rFSruoUihUZREPSL39UNdE3BBDu76
main network
private key
secret exponent: 32162737660659799401901343156672072893797470137297259782459076395168682141640
public pair x: 19122724810578381401279259492091176497647579703487086604820598127878910996497
public pair y: 93716738155005567718020901196556981584525395439024483644561058920479008416610
tree depth: 5
fingerprint: d69aa102
parent f'print: d880d7d8
child index: 1000000000
chain code: c783e67b921d2beb8f6b389cc646d7263b4145701dadd2161548a8b078e65e9e
WIF: Kybw8izYevo5xMh1TK7aUr7jHFCxXS1zv8p3oqFz3o2zFbhRXHYs
uncompressed: 5JMbvQZXHJAzJyoDnqWasGCwtiHJZivF2ckjn3n5mazYYtGNvJf
Bitcoin address: 1LZiqrop2HGR4qrH1ULZPyBpU6AUP49Uam
uncompressed: 1N7NsvfJJqhjjFp5R2X9FmBc8MLU7gxbsL
You can traverse the tree partially, and still get descendents from the child node. Here we see the path from the master M through 0/1/0/1 yields the same results as we get from going from M to 0/1/0, stopping there for a moment, then going to 1.
$ genwallet -f master-private-key -s 0/1/0 > m0,1,0
$ cat m0,1,0
xprv9xrdP7iD2L1YW43ygAskFNznwRQAFkb67X6vK5mJF1tdDQWXJdQnBjQqwYaHKPQ5wseEEDWmgBFpXmtxfGvAERhfiUZfoCyRfgMfGhPqx94
$ genwallet -f master-private-key -s 0/1/0/1
xprvA1fSfYjT9jfrP4WfUgMEcvTRYyQ6qoqRT2t7Z9qZ41TEG7egUv28pL5dHodAkrET8k7UqjzKRKCFUR1V36E9egU9sHoKXuiAFNbVsZdrnhj
$ genwallet -f m0,1,0 -s 1
xprvA1fSfYjT9jfrP4WfUgMEcvTRYyQ6qoqRT2t7Z9qZ41TEG7egUv28pL5dHodAkrET8k7UqjzKRKCFUR1V36E9egU9sHoKXuiAFNbVsZdrnhj
We’ve descended from master to 0/1/0/1 two ways. Same output.
You can strip out private key information, but still get the hierarchy of public keys.
$ genwallet -f master-private-key -s .pub > master-public-key
$ cat master-public-key
xpub661MyMwAqRbcFtXgS5sYJABqqG9YLmC4Q1Rdap9gSE8NqtwybGhePY2gZ29ESFjqJoCu1Rupje8YtGqsefD265TMg7usUDFdp6W1EGMcet8
$ genwallet -f master-public-key -s 0/2
xpub6AvUGrnEpfvJFYHymqh5qJ3V7qFyEFdpQom2tRQdV4Eo25kxagwHwVCMX1opKqAXxacHPAJafQW1uvH3bYQi1zbE5DMgXGAGNkHajLEuoa2
$ genwallet -f master-private-key -s 0/2.pub
xpub6AvUGrnEpfvJFYHymqh5qJ3V7qFyEFdpQom2tRQdV4Eo25kxagwHwVCMX1opKqAXxacHPAJafQW1uvH3bYQi1zbE5DMgXGAGNkHajLEuoa2
So public wallet keys can generate Bitcoin addresses. But getting WIF information requires the secret exponent, which has been stripped out.
$ genwallet -f master-private-key -s 0/2 -a
1J4LVanjHMu3JkXbVrahNuQCTGCRRgfWWx
$ genwallet -f master-public-key -s 0/2 -a
1J4LVanjHMu3JkXbVrahNuQCTGCRRgfWWx
$ genwallet -f master-private-key -s 0/2 -w
Kxtby4wzfHeCaRXma16dBNLgUE7Ct3Xkb6sRs3aZ56Bmtf1rcNWs
$ genwallet -f master-public-key -s 0/2 -w
can't generate WIF for public key
That means we can put a public wallet key on a web server, and even if a hacker steals it, all he (or she?) can do is generate the list of public keys. He can’t steal the Bitcoin since he has no access to the private keys. But keep those private wallet keys offline!!
We can generate uncompressed versions of Bitcoin addresses too, if you’re interested in that sort of anachronism.
$ genwallet -f master-private-key -s 0/2 -a -n
1HSEorKrq3DjqxtgETbLvnka62Wc4NZj3M
$ genwallet -f master-public-key -s 0/2 -a -n
1HSEorKrq3DjqxtgETbLvnka62Wc4NZj3M
$ genwallet -f master-private-key -s 0/2 -w -n
5JCEp99P8KGgKuEKFjARxpRrGgg1szDQUDCswqchLxYtrqZNgJh
Doesn’t it seem strange that the compressed WIF is longer than the uncompressed WIF? It’s true.
Private wallet keys have one additional power over public keys: only private wallet keys can generate children that use the “prime” directive. This derivation requires information about the secret exponent, which is stripped out of public keys. You can use this to generate change addresses, for example, which you probably want to keep slightly more private.
$ genwallet -f master-private-key -s 0p
xprv9uHRZZhk6KAJC1avXpDAp4MDc3sQKNxDiPvvkX8Br5ngLNv1TxvUxt4cV1rGL5hj6KCesnDYUhd7oWgT11eZG7XnxHrnYeSvkzY7d2bhkJ7
$ genwallet -f master-public-key -s 0p
can't derive a private key from a public key
You can strip it out later though, and you’re fine.
$ genwallet -f master-private-key -s 0p/5 > m0p,5
$ genwallet -f master-private-key -s 0p/5.pub > m0p,5.pub
$ genwallet -f m0p,5 -s 1 -a
1CxkGdM4oVdWdovcBHqUCeiUWUtN5EtR1a
$ genwallet -f m0p,5.pub -s 1 -a
1CxkGdM4oVdWdovcBHqUCeiUWUtN5EtR1a
In conclusion, this is pretty neat stuff.